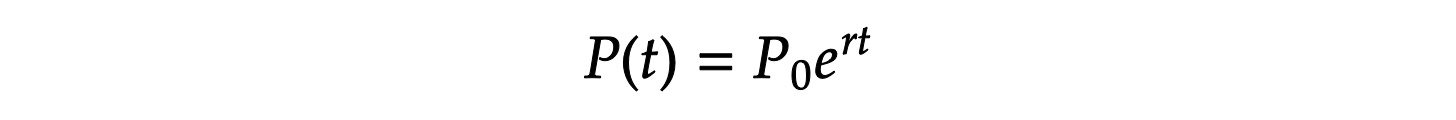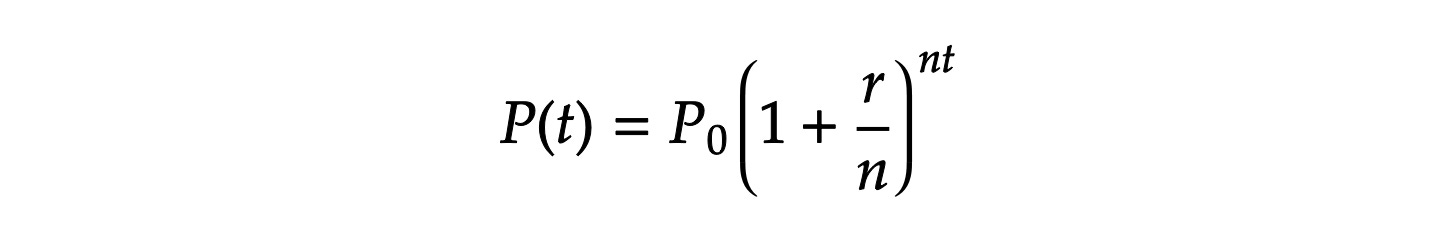Essay#1 如何成长
苏美尔平原的牛群给我们成长的启发
我想用这一篇通讯来探讨几件事情:
什么是心智模型
用复利的例子来理解心智模型
我们如何成长
透明盒子计划内容方面的侧重点
心智模型
英文是 mental model,其实是一个很直白的词。是指我们对现实事物其内在运作原理的认知。这些心智模型可以帮助我们更好地理解这个世界,推理我们的所作所为将如何影响我们周围的环境,使我们做出更好的决定,当然也会塑造我们的行为和人生。
对个人而言,最后的这一点尤为重要。不过在继续之前,我们不妨通过实例来解析一个心智模型,毕竟像上面那样解释就太形而上了。
复利
爱因斯坦称复利是“世界第八大奇迹”,即便在“爱因斯坦是否说过这话”的问题上存在争议,但人们对“复利是一个伟大发明”没有异议。本杰明·富兰克林设立了两个基金,就是为了向世人传授复利的魔力1。查理·芒格也在他的演讲中多次提到复利,当然他也是复利的践行者。
今天有无数的书和文章会举一个例子,如果你选择第一天得一美分,之后每天得前一天的一倍,30天内你可以比每天得1000美元的人获得多得多的钱(5368709.12美元)。大部分文章都是关于个人财务的,也有少部分会告诉你复利这种心智模型也可以被应用在生活的很多方面,但复利和那些“很多方面”的内在联系是什么?或者说复利的边界在哪里呢?
我们大多数人对复利的认知是跟今天的金融系统相关的,我一点也不怀疑有人会觉得复利的概念是银行家们发明的。就像新生代不知道为什么电脑里保存的图标要设计成磁盘的样子,因为他们压根没见过磁盘。想要探寻其根本,我们还得追根溯源,看看人类历史上关于复利的记载。
这是恩铁美那(Entemena)铭文锥体2,记录的是美索不达米亚平原南部两座城池之间的土地争夺战。乌玛城夺取了拉格什城一块沃土,在被抢占两代人后,拉格什的统治者恩美铁那夺回了土地,并要求乌玛以租金加利息的方式赔偿。其中利息的计算方式就是复利,当然因为使用了33.3%这么夸张的增长率,所以最后欠款是个天文数字,因此惩罚意义可能更多。不过逻辑上是完全合理的,恩铁美那的复利计算基础很简单,今年获得的利润谷物可用于明年的生产。史学家们推测,这种复利计算很可能受启发于苏美尔经济体系中另一种具有内在指数增长性质的生产活动:畜牧。
由此可以看出,复利的灵感正是来源于自然资源的生长。那种随着时间、按一定增长率增长的东西,或者说新产出的资源会被合入总生产资料以进一步再扩大产出的过程,符合这个描述的事物似乎都在复利这个心智模型的讨论范围内。而今天我们所熟知的金融行业的复利只是这种范型的一个例子。
至此我们回答了前面的问题。但我们仅仅知道一个心智模型“是什么”还不足以使之为我所用,我们还应该知道如何利用模型。因人而异,在这种时候我偏好用数学公式去理解,因为我觉得数学公式是最根本性的、无杂讯的描述。我们来看看复利公式(想划走的同学请留步,我保证没有什么数学基础也能看明白):
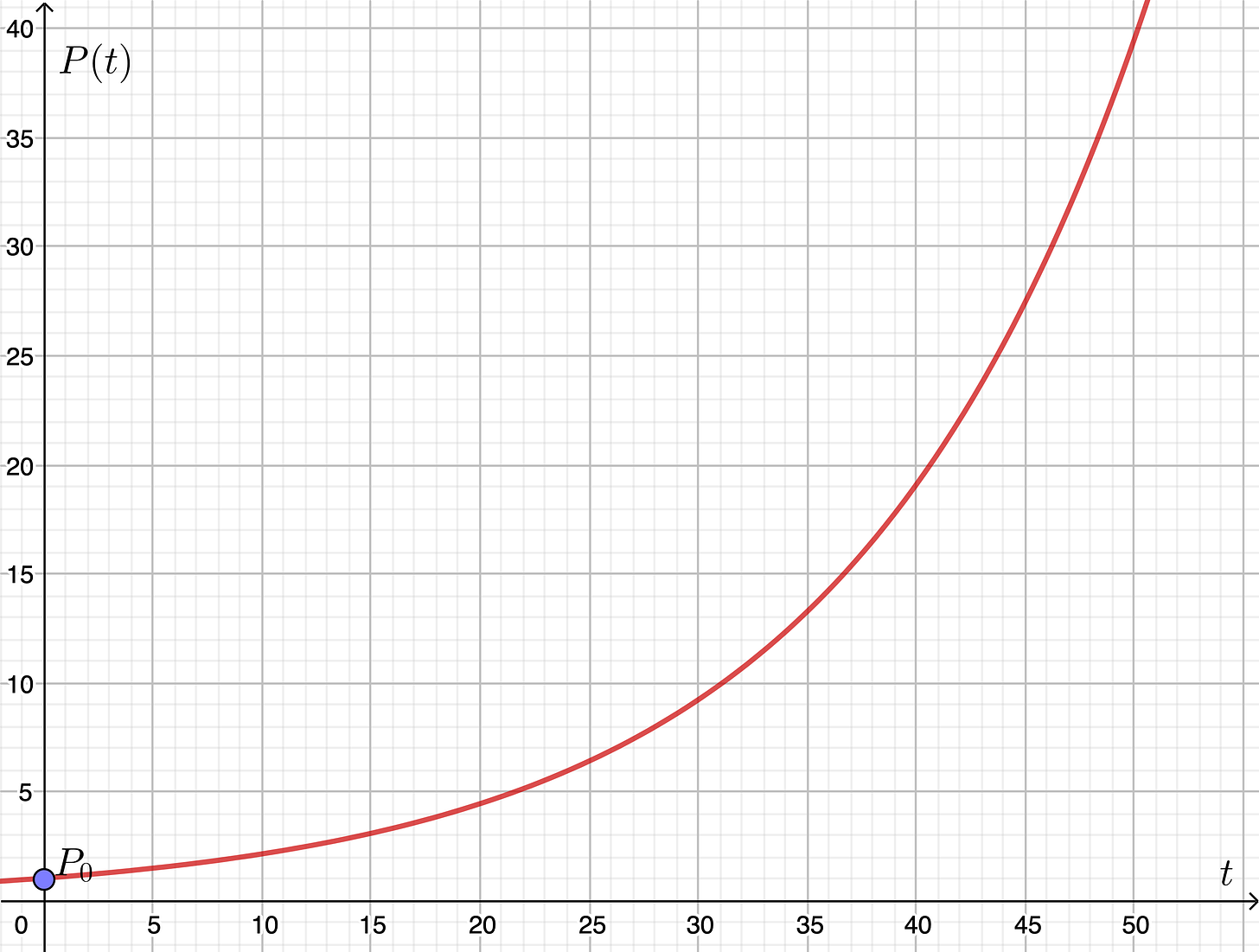
其中,t 是时间,r 是增长率,P0 是初始量,e 是自然常数(是个固定值,约等于2.718)。等号左边是最终结果,而右边则描述了各个影响因子及其内在关系。画成图就像这样:
t
时间是一个对所有人都很公平的变量,面对它,我们似乎无能为力,可真的是这样吗?有句英文谚语是这样说的:
The best time to plant a tree was 20 years ago. The second best time is now.
(最佳的种树时间是20年前,其次是现在。)
“即刻行动、为时不晚”可能是这句话的侧重点。但它同样也告诉了我们,面对符合复利条件的事物,越早开始、收获越大。
顺带一提,树的生长也是符合我们前面归纳的复利条件的。
r
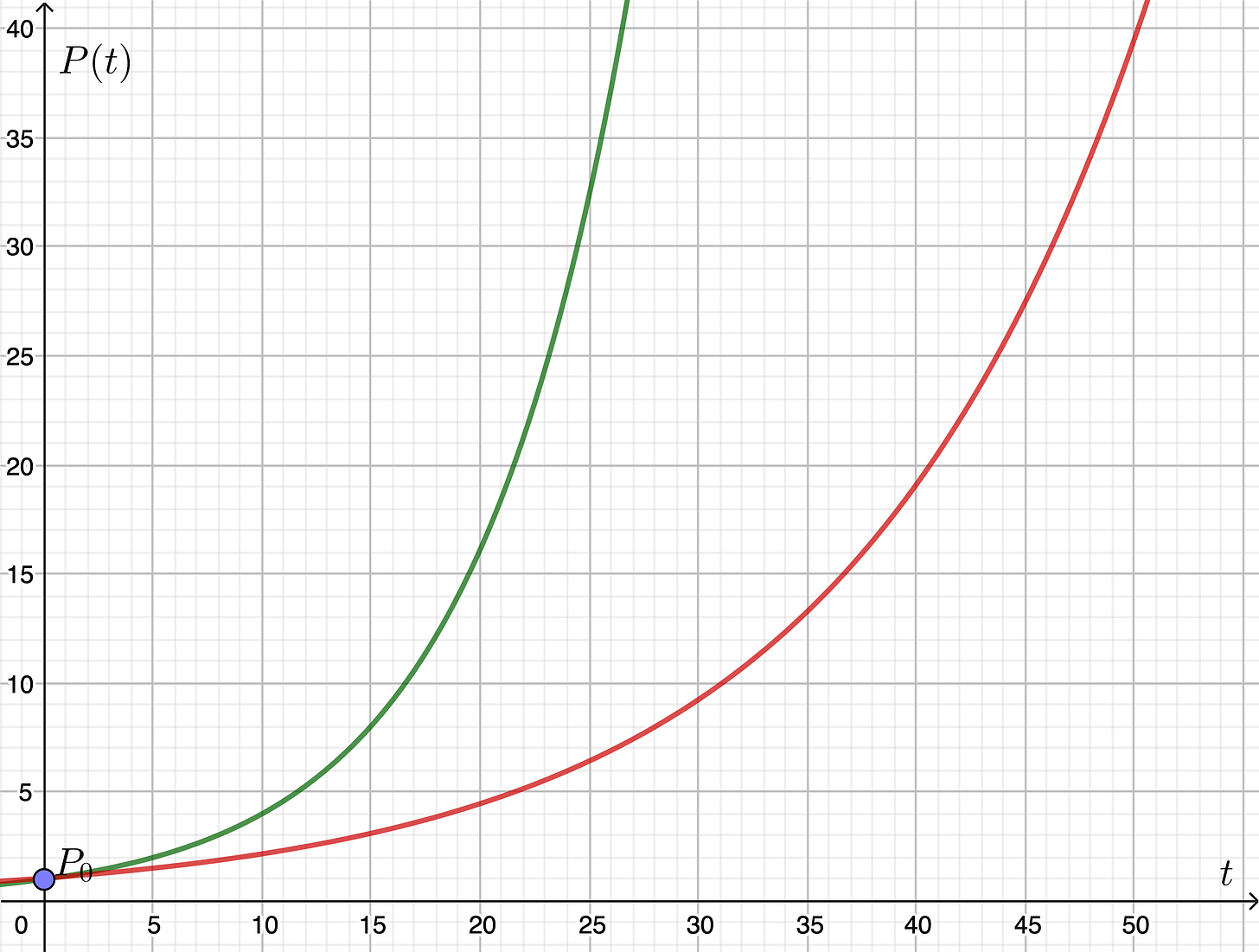
增长率相比较时间来说,可操作的东西就多了。但是我想这些操作无非分成这三类,正面影响、正交影响(即无用功,不产生任何影响)、和负面影响。事实上我们说的增长率就是这三种影响力之和。试想下面的这张示意图:
(红线和绿线有一样的初始值,但绿线比红线有更大的增长率)
引入的无用功和负面影响越多,增长越慢。为什么说引入无用功也会影响增长呢?我的想法是基于机会成本的预设的,即无用功所做的努力本可以用在更多的正面影响上。当然严格意义上来说,无用功是可以不参加讨论的。
关于 r 的另一个讨论是可持续性。复利很大地依赖于时间,如果一味追求 r 使系统奔溃、不再可持续,t 就被截短了,便再也没有复利可言。揠苗助长大概说的就是这个意思。
P0
无论从现实还是从数学的角度看,初始值其实在指数变量 r 和 t 面前就显得没那么重要,而且很多时候初始值是不受控的。我们就拿前面提过的钱和树当例子好了,你有多少钱或树苗有多大,都是现状和事实。你能做的非常有限。当然多多益善是一定的。
e
e 看起来是个常量,数值不会变,我们没啥能做的,但其实它来自另一个复利公式的变形(对数学不感冒的同学可以跳过这段,不会影响理解)。上面的那个是连续性复利公式,下面的这个是周期性复利公式。
其中新增变量 n 是结算利润、并将其加入本金的频率。两个公式看似不一样,但本质是一样的,前者是对后者的 n 求极限得来的。
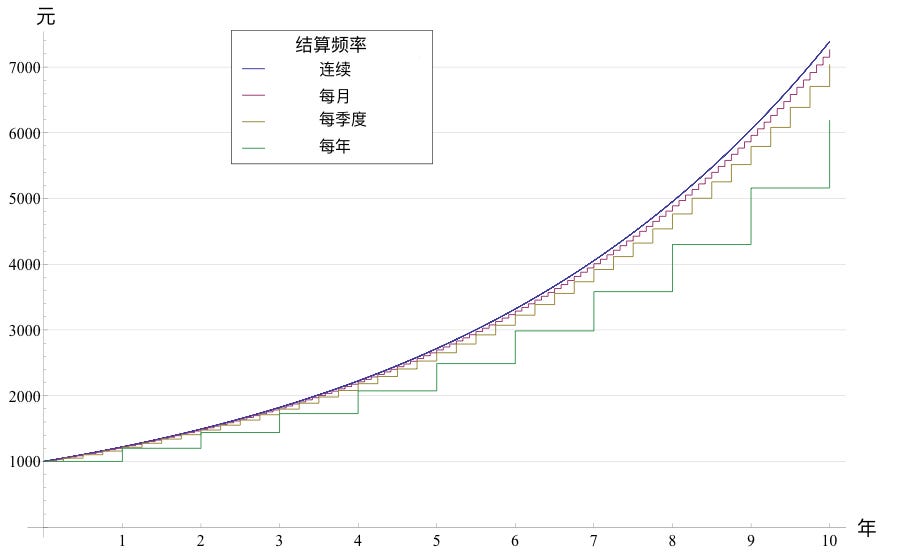
根据我们具体要讨论的复利模型情况而定,如果是周期性复利,结算频率越高,收益越大。下图我们以储蓄复利为例,看看连续性跟以月、季度和年结算的对比:
个人成长
就像“成长”这个词所暗示的一样,其内在是一种积累。本质上来说我们把以往获得的经验和教训应用到我们之后的人生中,以减少错误的决定、追寻更好的人生。我们不难看出它也在复利可应用的范畴内。
在个人成长中应用复利是一个不容易被践行的想法,因为近在眼前的快乐或利益在我们的脑中有更高的权重。它需要想象力、理性和坚持。在现在这个廉价多巴胺3到处都是的年代,实践复利变得尤为困难。但是在刚开头我们就说过了,心智模型可以塑造我们的行为。事实上,当我们意识到个人成长可以使用复利模型的时候,我们多多少少会修正我们的行为。
P0 和 t 就不在这里赘述了,我想具体说说 r(增长率)。个人成长很大程度上被我们所做的大大小小的决定主导,我们的生命体验也取决于这些决定和我们看待事物的方式。而决定也好、看待事物的方式也好,其核心都是由心智模型驱动的。因此我认为那些更接近真理的心智模型就是 r 里的那个正面影响力。
你可能猜到我想说什么了,有更接近真理的心智模型,就一定存在偏离真理的心智模型。没错,但偏离真理的心智模型并不是真正的负面影响力。导致偏离的罪魁祸首其实是各种各样的认知偏误(cognitive bias)。认知偏误是一种系统性的判断偏差,主要是人们以主观感受而非客观事实为基础建立心智模型所致。认知偏误有很多种类,成因也很多,以后我们会探索这个话题。
至此我们可以总结一下,就个人成长而言,不论起点如何(P0),我们需要持之以恒(t),运用更多接近真理的心智模型,极力避免认知偏误,把那些无用功的精力和时间省下来用在更具正面影响的事情上(r)。
透明盒子计划的内容
上一次通讯我只说了通过 Zettelkästen 的方式做读书笔记,并分享所读所想。但我没提分享什么样的内容。
个人成长的具体执行方面我帮不了什么忙,不过我可以帮助大家收集更多有价值的心智模型,揭示更多危险的认知偏误。我想尽可能通过我的阅读笔记在这里分享无杂讯的信息和经得起时间检验的智慧。我不会在这里聊政治和一些空洞无内容的东西。
在 Twitter 和电邮通讯的内容侧重方面,我打算以电邮为主体,推文为补充。就像上一期一样,主体是说 Zettelkästen 方法,推文里则提供了很多相关的补充材料。
话说回来,Zettelkästen 方法也是符合复利条件的,你发现了吗?
透明时间
自透明盒子计划启动之后,电邮通讯和 Twitter 都受到了很多关注,收到了热心读者们的来信。这些远在我期望之外,透明盒子计划也俨然成了一个小小社区。非常感谢大家!
截止到写稿时,我们这个小社区的电邮通讯有49人订阅,Twitter 有159人跟随。
我的初衷是以阅读笔记的方式来帮助自己成长,因此我不打算开启收费或捐赠。分享在这里,是因为我觉得对我有益的东西或许对别人也有益。如果你觉得我的分享有帮助到你,你真的真的想要回馈这个小小社区,请帮助她成长:分享通讯和推文给一位志同道合的朋友,或者给我反馈,让我们的小小社区变得更好😃
祝大家成长顺利,我们下次再见!
Peter Jeppson. "Benjamin Franklin’s Experiment with Compound Interest Will Astound You." Accessed Jun 6, 2020.
廉价多巴胺:源于创业家和投资人 Naval Ravikant,他曾说“The modern devil is cheap dopamine”,“There is so much cheap, instant dopamine and meaning, that it’s hard to motivate yourself to do the “real thing” any more – many teens struggle with this (as well as their parents)”。跟运动、读书和思考相比,刷社交网络和看短视频就是廉价得多的多巴胺。